오봉이와 함께하는 개발 블로그
동적 프로그래밍 기법 본문
728x90
Algorithmday_2 정리 (2021.11.29 월요일)
동적 프로그래밍 기법(Dynamic Programming)
- 분할 정복 기법과 유사하게 부분 문제의 해답을 이용하는 방식으로 문제를 해결하는 방식
- 주어진 문제를 여러 개의 소문제로 분할하여 문제를 해결
- 상향식 설계 기법
- 작은 문제부터 먼저 해결한 후 그 결과를 큰 문제에서 활용함으로써 효율성을 높이는 방법
동적 프로그래밍 방식 적용 방법
- 분할 정복식처럼 문제를 나눈 후 주어진 부분 문제들을 한 번 계산한 후에는 특정 장소에 저장
- 이 부분 문제의 해가 필요할 때 이를 다시 계산하지 않고 이전에 저장해둔 결과 이용
- 일반적으로 부분 문제의 값을 저장하는 장소는 배열 사용
분할 정복 기법 VS 동적 프로그래밍 기법
- 분할 정복 기법(하향식)
- 분할되는 소문제가 독립적이라 소문제를 재귀적으로 풀어 그 결과를 합침
- 중복된 계산이 계속 발생
- 중복 문제를 방지하기 위해 동적 프로그래밍 기법 사용
- 동적 프로그래밍 기법(상향식)
- 부분 문제의 해답을 이용하는 방식으로 문제 해결(분할 정복 기법과 동일)
- 소문제의 계산 결과로 표(배열)에 저장해 놓고 필요할 때 저장된 값 사용
- 따라서 중복 계산을 하지 않는다
동적 프로그래밍 적용 대상
- 최소치 또는 최대치를 구하는 최적하 문제에 적용
- 최적해는 기본적인 소문제의 최적해로부터 더 큰 크기의 소문제의 최적해를 구하는 과정을 거침
- 최적화 문제의 최적해는 여러 개가 있을 수 있지만 그 중 하나를 구하면 됨.
동적 프로그래밍 방법 적용 예
- 피보나치 수열
- 조약돌 놓기 문제
- 행렬 경로 문제
- 연쇄 행렬 곱셈
- 이항 계수
- 최단 경로 구하기
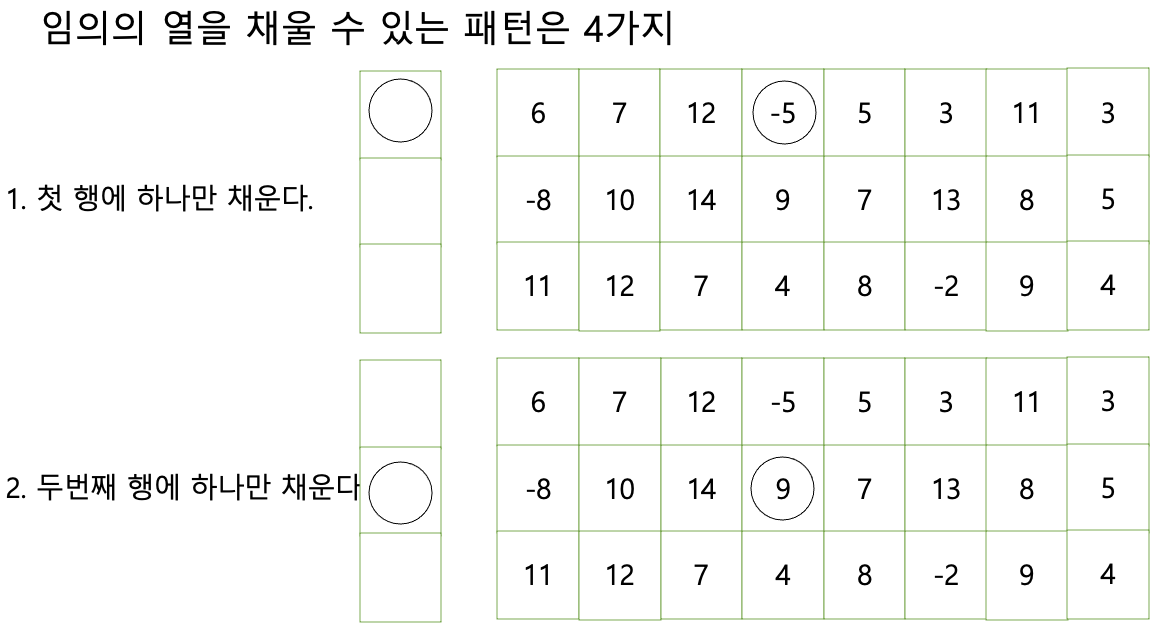
조약돌 놓기 문제
- 조약돌을 놓는 방법(제약조건)
- 각 열에 적어도 하나의 조약돌을 놓아야 한다.
- 가로나 세로에 인접한 두 칸에 동시에 조약돌을 놓을 수 없다.
- 목표 : 돌이 놓인 자리에 있는 수의 합을 최대가 되도록 조약돌 놓기




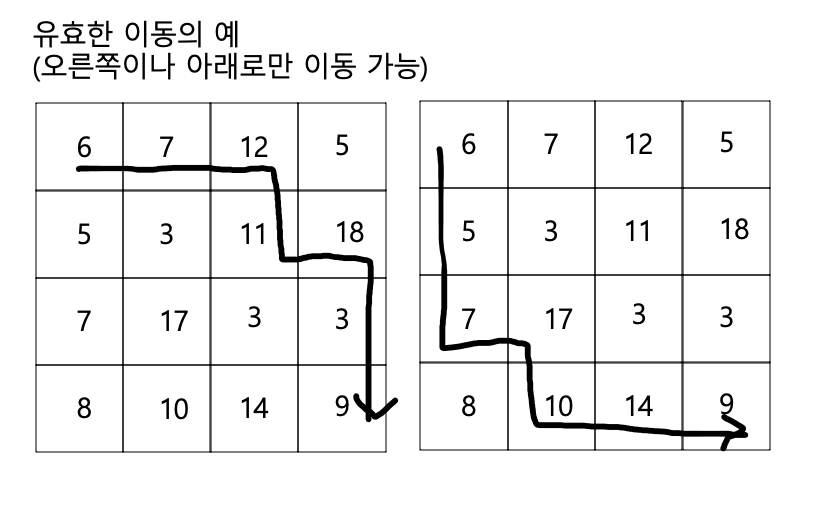
행렬 경로 문제
- 양수 또는 음수 원소들로 구성된 (n,n)행렬
- 행렬의 좌상단에서 시작하여 우하단까지 이동
- 제약 조건
- 오른쪽이나 아래로만 이동 가능
- 왼쪽, 위, 대각선 이동 불가
- 목표
- 행렬의 좌상단에서 시작하여 우하단까지 이동하되
- 방문한 칸에 있는 수들을 더한 값이 최소가 되도록 한다.

728x90
'알고리즘 & 자료구조 & 네트워크' 카테고리의 다른 글
| 자료구조 데크(deQue) (0) | 2021.11.29 |
|---|---|
| 자료구조 큐(Queue) (0) | 2021.11.29 |
| 자료구조와 스택 (0) | 2021.11.29 |
| Greedy기법(최단 경로, 최소 신장 트리) (0) | 2021.11.29 |
| 알고리즘 기초와 간단한 사례 (0) | 2021.11.26 |
Comments



