오봉이와 함께하는 개발 블로그
해싱(Hashing) 본문
728x90
Algorithmday_4 정리 (2021.12.01 수요일)
해싱(Hashing)
- 해시 함수와 해시 테이블을 이용하여 데이터를 빠르게 저장하고 탐색하는 방법
- 데이터를 해시 테이블이라는 배열에 저장하고 데이터의 키 값으로 해시 함수를 통하여 테이블의 주소를 반환해서 원하는 데이터를 찾는 방식
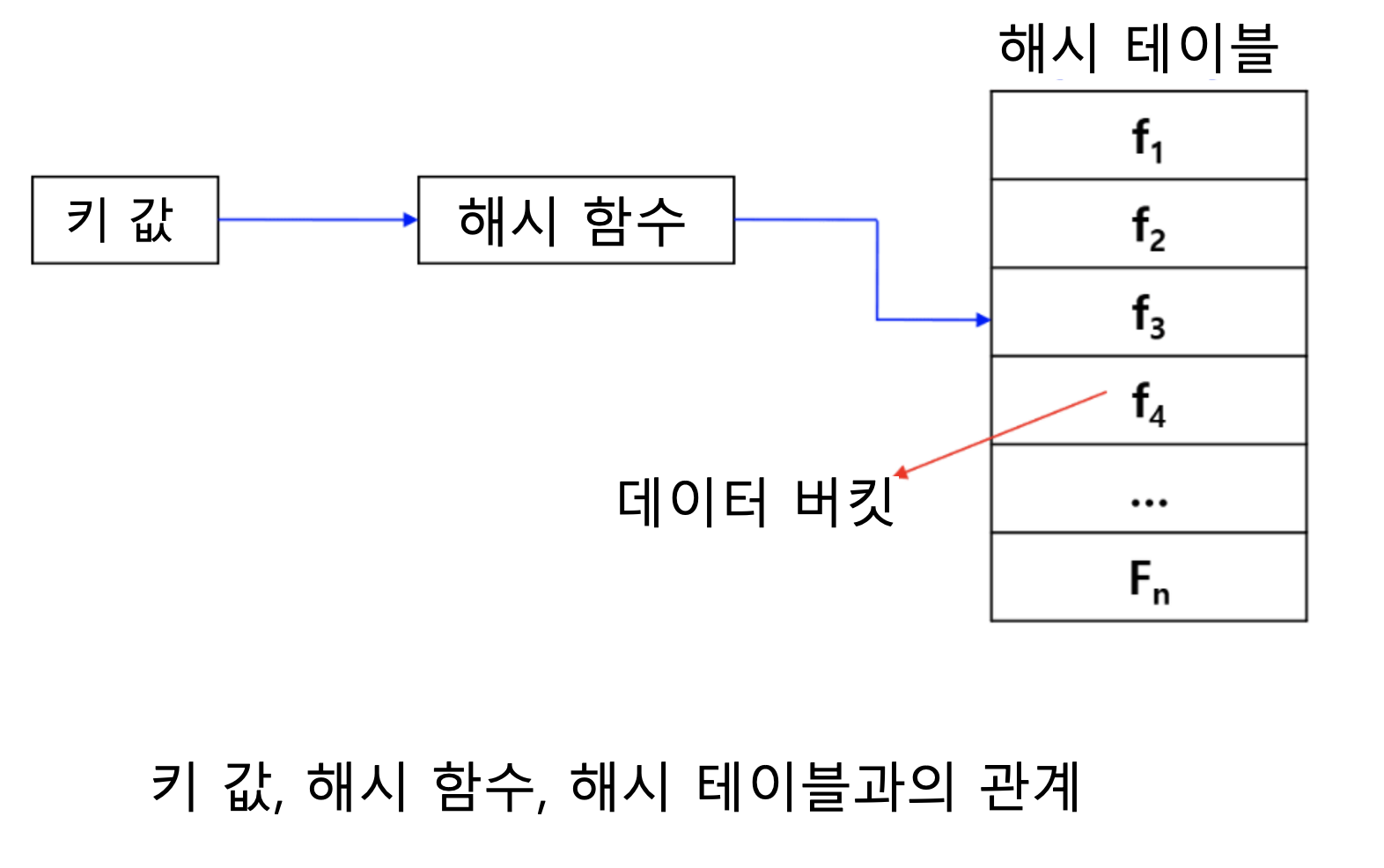
해시 테이블
- 값의 연산에 의해 직접 접근 가능한 구조
해시 함수
- 해시 테이블에서 키 값을 주소로 변환하는데 사용되는 함수
- 계산이 빠르고 간단해야 하며, 다른 키 값이 같은 주소를 산출하는 경우가 적어야 함
해시 함수 종류
- 나눗셈법
- 중간 제곱법
- 폴딩법
- 기수 변환법
- 자리수 분석법
나눗셈법
- 키 값을 정수로 보고 이를 적당한 양의 정수(주소, 해시 테이블의 크기 등)로 나누어서 그 나머지를 해시 주소로 하는 방법
- h(k) = k mod n
- h() : 해시 함수
- k : 키 값
- n : 나누는 수
- 특징
- 주소 계산법이 매우 간단하지만 나누는 수 n을 적당하게 선택하는 것이 쉽지 않음
- n 선택 시 고려 사항
- n 값은 충돌 발생의 가능성을 최소화하도록 선정
- 따라서 나누는 값 n은 소수로 정하는 것이 좋다
- 나눗셈법 예
- 키 값 : 172148
- 주소 공간 영역 : 7000
- 주소 공간 영역에 가까운 소수 : 6997
- 해시 주소 : 4220
- 172148 / 6997 = 몫 : 24, 나머지 4220
중간 제곱법
- 키 값을 제곱한 다음 그 제곱값의 중간 부분의 적당한 자리수를 해시 주소로 정하는 방법
- 중간 제곱법 예
- 키 값 k = 7642
- k^2 = 58247424
- 해시 테이블의 주소 : 2474
- 58 2474 24
폴딩법
- 키를 같은 크기의 부분으로 나누고(접고), 이들을 모두 더하거나 XOR등을 취하여 해시 주소를 정하는 방법
- 이동 폴딩법
- 오른쪽 끝을 맞추어 더한 값을 해시 주소로 정하는 방법
- 탐색키 : (1 2 3 | 2 0 3 | 2 5 1 | 1 6 2 | 1 0)
- 123 + 203 + 251 + 162 + 10 = 740
해시 충돌
- 해시 테이블에 데이터를 삽입할 때 서로 다른 데이터가 같은 주소에 배당되는 것
- 오버플로우 라고 하기도 한다.
- 해결법
- 선형 조사법
- 2차 조사법
- 체이닝
선형 조사법
- 충돌이 일어난 항목을 해시 테이블의 다른 위치에 저장하는데 충돌이 발생한 자리에서 그 다음 버킷들을 차례로 하나씩 조사하여 최초로 나오는 빈 버킷에 데이터를 삽입
- 장점
- 주소 계산 간단
- 단점
- 조사 시간 많이 걸림
- 해시 테이블 상 데이터의 위치가 일정한 키에 의해 집단으로 뭉치는 경향 발생
2차 조사법
- 충돌이 발생했을 때 원래 주소로부터 2차 함수 되는 거리만큼 떨어진 곳을 차례로 탐색해서 최초로 나오는 빈 곳에 데이터 삽입
- 장점
- 주소 계산 간단
- 데이터들의 위치가 일정한 키를 중심으로 뭉치려는 경향을 어노 정도 배제할 수 있다.
- 단점
- 해시 테이블 모든 버킷이 다 조사되지 않는다.
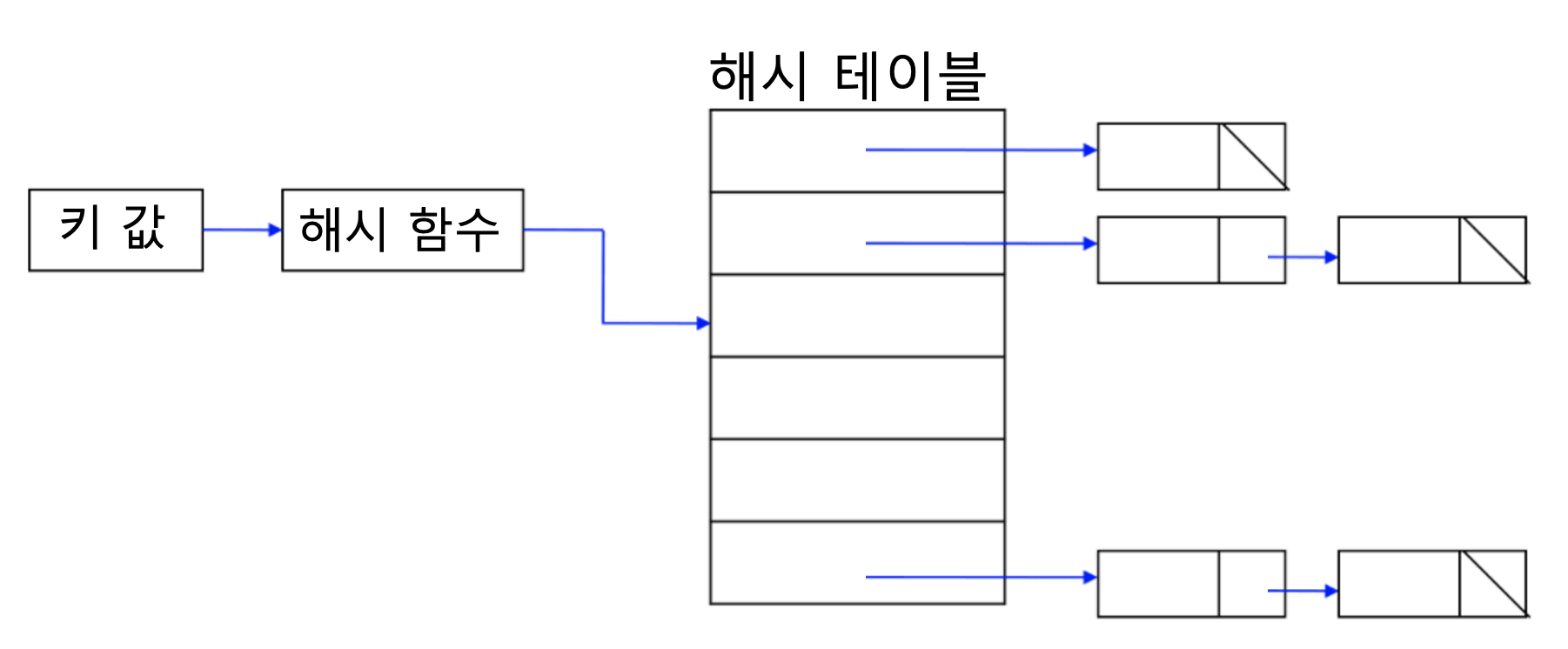
체이닝 법
- 각 버킷에 삽입과 삭제가 용이한 연결 리스트를 구성하는 방법
- 해시 테이블 자체는 포인터의 배열로 만들고, 같은 버킷에 해당되는 데이터들을 체인(연결리스트)로 만들어서 연결
- 장점
- 삽입, 삭제 시 문제 없음
- 단점
- 포인터 연산이기 때문에 동적인 기억 장소 할당 필요
- 링크 필드로 사용되는 부가적인 기억 장소 필요
728x90
'알고리즘 & 자료구조 & 네트워크' 카테고리의 다른 글
| 이진 탐색 트리 - 추가, 삭제, 검색, 전체 순회 (0) | 2021.12.05 |
|---|---|
| Quick Sort - 배열 크기 입력, 0번 부터 값 입력, 내림차순 출력 (0) | 2021.12.05 |
| 탐색(Search) - 순차, 이진, 보간, 이진 트리 (0) | 2021.12.01 |
| 힙 정렬(Heap Sort) (0) | 2021.12.01 |
| 기수 정렬(Radix Sort) (0) | 2021.12.01 |
Comments


