오봉이와 함께하는 개발 블로그
트리(Tree) 본문
728x90
Algorithmday_3 정리 (2021.11.30 화요일)
Tree
- 트리
- 자료들의 항목이 가지들로 연결될 수 있게 자료가 구성되어 있는 구조
- node(자료(항목))와 edge(간선(가지))로 구성.
- 계층적인 구조
- 부모-자식 관계의 노드들로 구성

트리의 용어
- 노드(node) : 트리를 구성하는 각 자료 항목
- 근 노드(root node)
- 트리 구조를 시작하는 노드
- 최상위에 존재하는 하나의 노드
- 자식 노드
- 임의의 노드에 연결된 다음 레벨의 노드들의 집합
- D의 자식 노드는 H, I, J
- 부모 노드
- 임의의 노드에 연결된 상위 계층의 노드
- B는 E, F의 부모
- 차수(degree)
- 한 노드에 연결된 가지의 수 (노드가 갖고 있는 자식 노드의 개수)
- D의 차수는 3
- 레벨(level)
- root node부터 0으로 시작해서 아래 가지로 갈수록 레벨이 1씩 증가함
- F는 레벨 2
- 트리의 깊이(depth)
- 어떤 특정 노드에서 root node에 이르는 경로의 길이
- F의 깊이 : 2
- L의 깊이 : 3
- 레벨 값 = 깊이 값
- 트리의 높이(height)
- 트리의 최대 레벨 + 1
- 사진의 트리는 높이가 4인 트리다.
- 근 노드(root node)
트리 구조의 저장
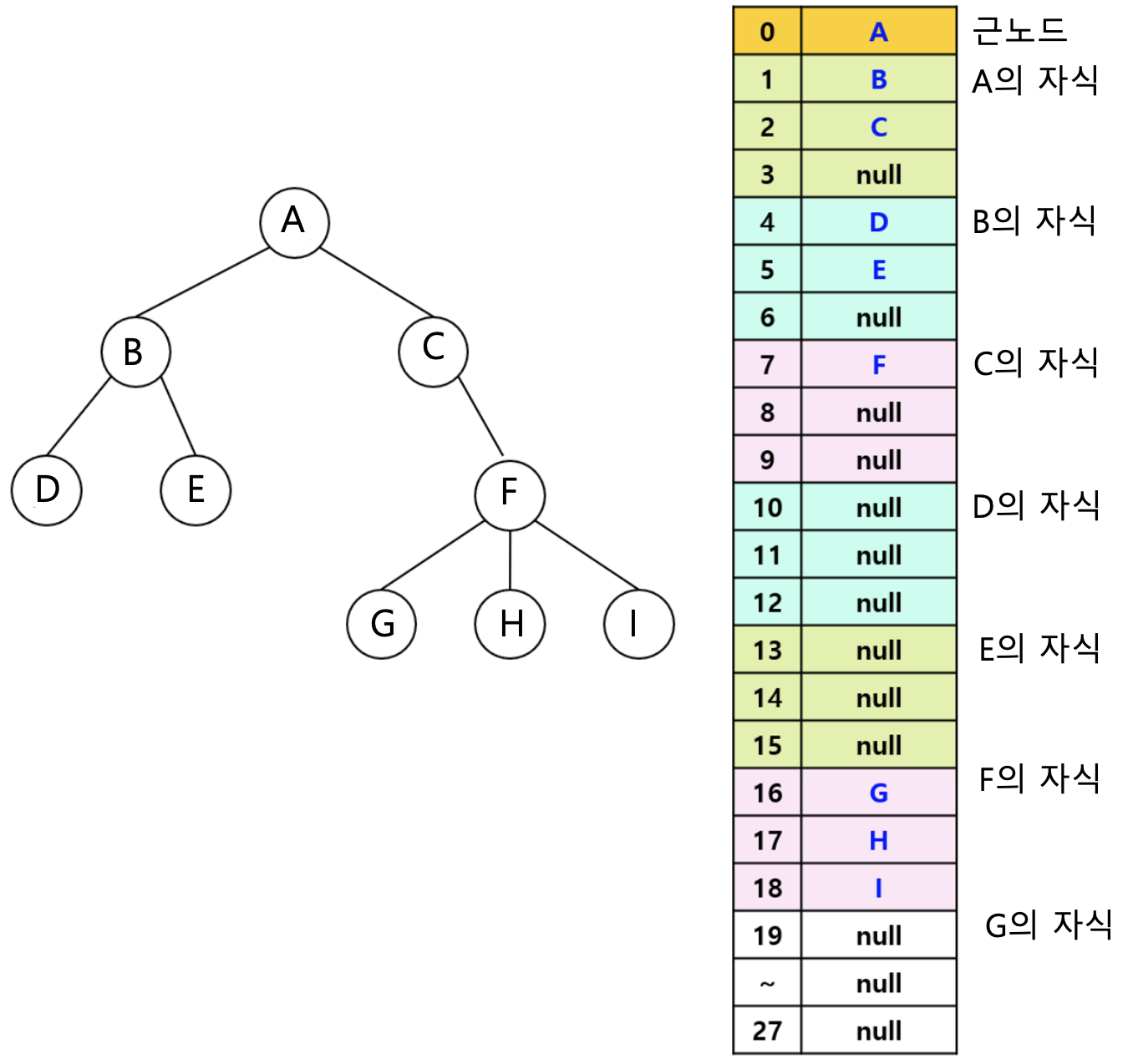
- 배열을 이용한 방법
- 연속적인 기억 공간을 그대로 이용하는 배열의 구조에 트리를 저장
- 각 노드 당 최대 차수 3만큼 기억 장소 확보
- 최대 기억 장소 : 총 노드의 개수(9) x 트리의 차수(3) + 1 = 28
- 연결 리스트를 이용한 방법
이진 트리
- 왼쪽 서브 트리와 오른쪽 서브 트리라고 부르는 2개의 분리된 트리로 구성된 노드들의 유한 집합
- 이진 트리는 모든 노드들의 차수는 2를 초과할 수 없음
- root 노드만 있어도 이진 트리로 인정
- 왼쪽과 오른쪽의 반향성 존재
- 트리 (a)와 트리 (b)는 다른 트리

- 서브 트리가 왼쪽이거나 오른쪽이 아닌 아래로 향한 트리는 이진 트리가 아님

트리의 운행(Tree Traverse)
- 트리 구조의 각 노드를 전부 한번씩 방문하여 검색해내는 방법
- 레벨 순서 운행 방법
- 상향식 레벨 순서 운행법
- 하향식 레벨 순서 운행법
- 노드 위치에 따른 운행벅
- 전위 / 중위 / 후위 운행법
- 이진 트리의 운행법
- 일반적인 트리의 운행보다 간단
- 나타낼 수 있는 조합의 수는 여섯 가지이지만, 왼쪽 서브트리가 오른쪽 서브트리보다 선행한다는 제약을 주면 3가지 운행법만 존재
- 전위 : root - left - right
- 중위 : left - root - right
- 후위 : left - right - root
전위 운행
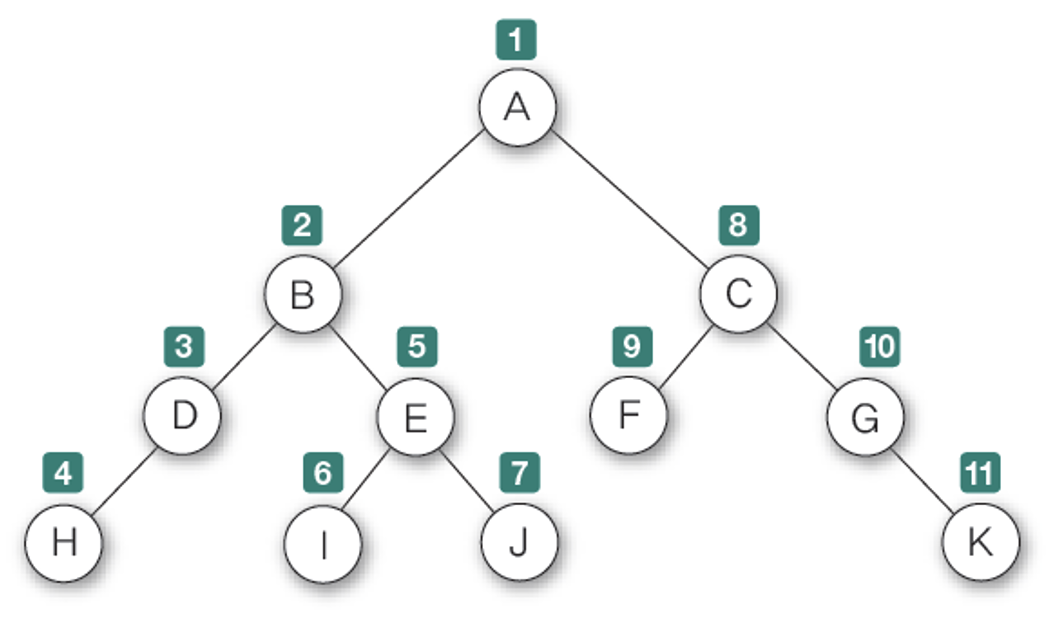
- 경로 : A - B - D - H - E - I - J - C - F - G - K
중위 운행

- 경로 : H - D - B - I - E - J - A - F - C - G - K
후위 운행

- 경로 : H - D - I - J - E - B - F - K - G - C - A
728x90
'알고리즘 & 자료구조 & 네트워크' 카테고리의 다른 글
| 버블 정렬(Bubble Sort) (0) | 2021.12.01 |
|---|---|
| 정렬(Sort) (0) | 2021.12.01 |
| 컬렉션 프레임워크 - Map(HashMap) (0) | 2021.11.30 |
| 컬렉션 프레임워크 - Set(HashSet) & Iterator (0) | 2021.11.30 |
| 컬렉션 프레임워크 - Vector (0) | 2021.11.30 |
Comments

